Sobald eine Diskussion um Grafikkarten losgeht, ist man ganz schnell auch bei Begriffen, die nicht mehr viel mit den Grafikkarten selbst zu tun haben, sondern mit dem, was Grafikkarten so bearbeiten: Polygone, Vektoren, Matrizen, Rasterizer, Grafikengines etc. Eine Grafikkarte ist eben immer nur Mittel zum Zweck, um etwas zu erreichen – in diesem Fall die Beschleunigung speziell der Grafikengine eines Spiels. Doch wie funktionieren heutige Grafikengines eigentlich? Hierzu soll dieser Artikel einen kurzen Einblick liefern ...

1.
Einleitung – oder: Historisches

(Spätestens) seitdem erste Computerspiele das Licht der Welt erblickten, musste Grafik auf den Bildschirm gezeichnet werden. Wenn man der Definition des Begriffs "Grafikengine" folgt, welchen die Wikipedia gibt, so ist eine Grafikengine "ein mitunter eigenständiger Teil eines Computerprogramms oder einer Computer-Hardware, welcher für dessen Darstellung von Computergrafik zuständig ist […]". So gesehen hatten selbst Spiele wie Pong, Space Invaders oder Pac-Man Grafikengines.

Diese und auch fast alle anderen Spiele, die auf Homecomputern wie dem C64 oder auf Konsolen wie dem NES verfügbar waren, verwendeten 2D-Grafik. Dabei wurde praktisch alles "per Hand" gezeichnet: Hier eine Wolke, da ein Baum, dort ein Strichmännchen. Die dafür nötigen Grafiken wurden per Code erzeugt oder kamen aus Bitmaps. Außerdem kamen Sprites zum Einsatz. Solche Spriteengines wurden immer weiter entwickelt, verbessert, verfeinert. Ihren Höhepunkt fanden sie vielleicht in Spielen wie denen der Turrican-Reihe.

Auf späteren Systemen wie dem Amiga 500 oder dem SNES sollte jedoch nach und nach statt der mittlerweile althergebrachten, spritebasierten 2D-Grafik nun 3D-Grafik zum Einsatz kommen. Die Sprite-Technik war leistungsfähig, für 3D aber vollkommen ungeeignet. Gerade am SNES wurde das Dilemma deutlich: War die Hardware des SNES noch sehr auf Spritedarstellung getrimmt, zeigten doch Erfolge wie der des legendären Mario Kart, wie gut 3D bei den Spielern ankam.

Für eine "echte" 3D-Darstellung war die damalige Hardware jedoch viel zu langsam. Spieleentwickler begannen, das zu tun, was sie schon immer taten: Tricksen!

Auch am PC wurde getrickst, was das Zeug hielt: Es kamen ganz unterschiedliche Ansätze zum Vorschein, dreidimensionale Grafiken zu erzeugen, und keine davon lieferte "echtes" 3D. Das berüchtigte Wolfenstein 3D setzte eine "Raycasting" genannte Technik ein, die später erheblich weiterentwickelt wurde und sich lange als die Technik für Egoshooter zu etablieren schien.

Als Alternative bot sich die voxelbasierte Grafik an, die u.a. Comanche nutzte. Und natürlich gab es auch schon früh polygonbasierende 3D-Grafik. Selbst auf dem C64 war hierfür Stunt Car Racer verfügbar!

Wann nun "echtes" 3D erreicht wird, ist streitig. Momentan lässt Intel verstärkt an Raytracingengines für Computerspiele forschen, weil Raytracing oft als einzige "echte" 3D-Berechnungsmethode angesehen wird. Im Kino läuft "Avatar", die Unterhaltungsindustrie hofft auf "3D" als den nächsten Kassenfüller.

Fakt ist aber, dass als Prinzip für die Grafikberechnung bei Computerspielen die Polygongrafik (eigentlich: Polygonrasterung) als Sieger aus den Achtziger- und Neunzigerjahren hervorgegangen ist. Praktisch jedes 3D-Spiel verwendet heute Polygongrafik. Hauptgründe für deren Sieg sind wohl zum einen die Tatsache, dass Polygongrafik gut und schnell mittels massiver paralleler Numbercruncher (GPUs) zu berechnen ist, zum anderen kommt Polygongrafik "echtem" 3D doch recht nah: Zumindest als mathematisches Konstrukt wird ein echter dreidimensionaler Raum vorgehalten. Dennoch wird auch heute noch getrickst, wo es nur geht …

2.
Mathematik – oder: So einfach funktioniert die Welt

Um geschickte Trickserei soll es hier aber gar nicht gehen. Polygongrafikengines haben eine langjährige Entwicklung hinter sich: Von Stunts ...

... bis zu Crysis ...

... und darüber hinaus. Doch wie funktioniert die Technik?

Wie der Name schon sagt, wird in der Polygongrafik die Grafik aus Polygonen (dt: Vielecken) zusammengesetzt, sogenannten "Primitives". Wenn mehrere solcher Vielecke zu einem Netz (eng: Mesh) zusammengesetzt werden, ergibt sich ein Drahtgittermodell eines dreidimensionalen Objektes, welches dann gerendert wird. Wie dies gemacht wird, soll im Folgenden beschrieben werden.

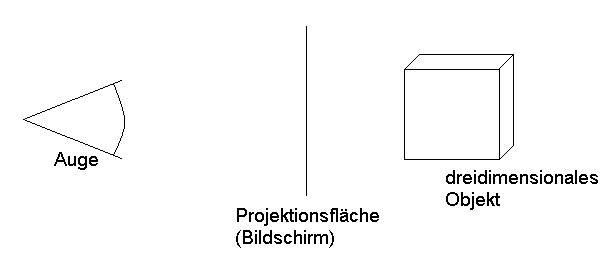
Zunächst einmal muss klargestellt werden, dass die dreidimensionale Welt "im" bzw. "hinter" dem Bildschirm stattfindet. Stellt man sich den Bildschirm als eine der Flächen eines Würfels vor, so befindet sich im Inneren des Würfels die dreidimensionale Welt. Der Bildschirm ist nur unser Fenster, durch das wir in die Welt im Würfel hineinschauen können.

Die dreidimensionale Welt, die sich im Inneren des Würfels abspielt, hält der Computer in seinem Arbeitsspeicher vor. Genauer gesagt befindet sich im Arbeitsspeicher die dreidimensionale Koordinate eines jeden Eckpunktes eines jeden Polygons der dreidimensionalen Welt. Bewegt sich ein Objekt durch den Raum, werden die Koordinaten der Polygone des betreffenden Objekts entsprechend angepasst. Der Renderer kann dann auf Basis der neuen Daten eine aktualisierte Ansicht unseres Fensters in die Welt berechnen. Es findet eine Projektion statt: Die dreidimensionale Welt wird auf die zweidimensionale Bildschirmoberfläche projiziert.

Üblicherweise werden 3D-Modelle mithilfe einer Modeling-Software wie Blender erzeugt. Hier soll stattdessen ein einfaches Modell "per Hand" definiert werden. Eine quadratische Pyramide soll es sein. Dazu ist ein Quadrat nötig und nur zwei Dreiecke (!), da die Seiten nicht gefüllt werden sollen (der Trick sollte niemandem auffallen, wir verraten es einfach keinem). Das ergibt genau drei Polygone, die zusammen ein Mesh bilden werden.

Hinweis: Mit diesem Mesh würde man bei Direct3D schon nicht sehr weit kommen. Direct3D setzt nämlich voraus, dass alle Polygone aus drei und nur aus drei Ecken bestehen (also Dreiecke sind). Die Grundfläche der Pyramide soll aber ein Quadrat sein. Deswegen wäre es zunächst nötig, das Quadrat in zwei Dreiecke zu zerlegen (zu "triangulieren"). Dieses Erfordernis macht Direct3D aus guten Gründen: Zum einen wird somit eine Einheitlichkeit der Berechnungsalgorithmen ermöglicht, zum anderen wird so sichergestellt, dass Polygone stets konvex sind.

Hier zunächst die vier Koordinaten des Quadrats Q:

     

Das Quadrat liegt also auf der x-y-Ebene, die Höheninformation z ist für alle Punkte gleich null. Die Mitte des Quadrats ist genau der Ursprung (0, 0, 0). Für die Spitze der Pyramide bietet sich also ein Punkt an, der genau über der Mitte liegt, nur eben hoch genug. So sind auch die beiden Seitenflächen der Pyramide definiert.

Dreieck A:

   

und Dreieck B:

   

3.
Punktevergabe – oder: Ran an's Eingemachte

Bis jetzt besteht die Welt aus fünf Punkten, die durch dreidimensionale Vektoren dargestellt werden. Um diese dreidimensionalen Vektoren sinnvoll auf dem Bildschirm darstellen zu können, bedarf es einer Projektion. Um eine solche Projektion durchführen zu können, wird eine Projektionsmatrix benötigt. Diese Matrix bildet die dreidimensionalen Vektoren in den zweidimensionalen Raum ab, indem die Vektoren mit der Matrix multipliziert werden.

Matrizen werden multipliziert, indem ihre Elemente paarweise multipliziert und zeilen-/spaltenweise aufaddiert werden. Dieses kurze Beispiel enthüllt schon das ganze Geheimnis.

Hinweis: Bei der Polygongrafik sind enorm viele solcher Matrixmultiplikationen vonnöten. Man sieht, dass hierfür ausschließlich die Grundrechenarten Multiplikation und Addition benötigt werden. Frühe Grafikbeschleuniger (zu 3fdx-Zeiten) waren simple multiply/add-Maschinen. Heutige Grafikkarten können mehr, da sie auch mehr Aufgaben bekommen, ihre wesentliche Hauptaufgabe ist aber nach wie vor massives Multiplizieren und Addieren. Die Berechnungen sind dabei in aller Regel voneinander unabhängig, so dass viele Berechnungen parallel ablaufen können. Moderne GPUs rechnen eine MUL und eine ADD (auch zu einer MADD zusammengefasst) pro Takt und Paralleleinheit. So kommen viele hundert Milliarden MADDs pro Sekunde zustande.

Wenn der (transponierte) Vektor A die Dimension 1x3 hat und das Ergebnis der Multiplikation die Dimension 1x2 haben soll, wie muss dann die Dimension der Projektionsmatrix P beschaffen sein?

Nach kurzem Hinschauen wird klar, dass als Dimension für P nur in Frage kommt. Jede Matrix P, die diese Eigenschaft erfüllt, ist Projektionsmatrix. Welche Matrix man wählt, entscheidet darüber, welche perspektivische Verzerrung man erhält. Somit kann man z.B. auch das Field of View (FOV) einstellen.

Eine einfache Projektionsmatrix ist die Kavalierprojektion. Diese Matrix sieht wie folgt aus:

Wenn also beispielsweise der erste Punkt des Grundquadrats der Pyramide auf die Ebene projiziert werden soll, ergibt sich:

Der Punkt (1,5 ; 0,25) lässt sich direkt auf das zweidimensionale Koordinatensystem zeichnen. Macht man das für alle Punkte der Szene, erhält man lauter Punkte auf der zweidimensionalen Ebene, die man nur noch so miteinander verbinden muss, wie es eine Vorschrift angibt. Diese Vorschrift ist in der Regel für jedes Polygon gegeben durch "verbinde Punkt eins mit Punkt zwei, Punkt zwei mit Punkt drei und Punkt drei mit Punkt eins". Beim hier verwendeten Grundquadrat muss das Ganze natürlich auf vier Punkte ausgeweitet werden – ein weiterer Grund, warum Direct3D hier nur Dreiecke zulässt: Damit diesbezüglich gar nicht erst Verwirrung aufkommt.